Pentedattilo
Durante gli anni trascorsi in Italia, ogni primavera, per circa due mesi, Escher si metteva in viaggio. Via nave, via treno, ma per lo più a piedi e con lo zaino in spalla, Escher si muoveva verso le regioni meridionali per raccogliere impressioni e fare schizzi di luoghi fino a quel momento a lui sconosciuti.
Frutto di questi viaggi, spesso avventurosi e disagevoli, sono alcune incisioni tratte dai disegni panoramici di Pentedattilo, ai piedi dell'Aspromonte: un suggestivo borgo calabrese arroccato su una rupe dalla caratteristica forma di cinque cime appuntite che si ergono come dita gigantesche.
Affascinato dalle rocce antropomorfiche e dalla fusione armoniosa del centro abitato con il paesaggio circostante, l'artista descriverà nei suoi diari l'atmosfera dell'incontro con la Calabria e con la sua gente come una parte indelebile dei suoi anni italiani:
“I nostri capelli biondi, gli abiti stranieri, lo strano bagaglio, devono aver fatto nascere una notevole diffidenza. Sono convinto che ci hanno sospettato di “iettatura” e di “malocchio”. (…) In quel momento quasi solennemente, Robert Schiess, calmo, tirò fuori dalla custodia la sua cetra e cominciò a pizzicare le corde sommessamente. (…) Quando il suonatore di cetra si fermò e si guardò intorno, c'erano intorno a lui un bel po' di spettatori che scoppiarono in applausi fragorosi. Ecco che le lingue si erano sciolte. Chi siete? Da dove venite? Che cosa fate qui? Dove siete diretti? Ci invitarono a bere vino (…), il che non potè che migliorare le nostre relazioni.”
La musica, con il suo linguaggio universale, si era mostrata come sempre l'antidoto speciale per spezzare l'incantesimo dell'ostilità.

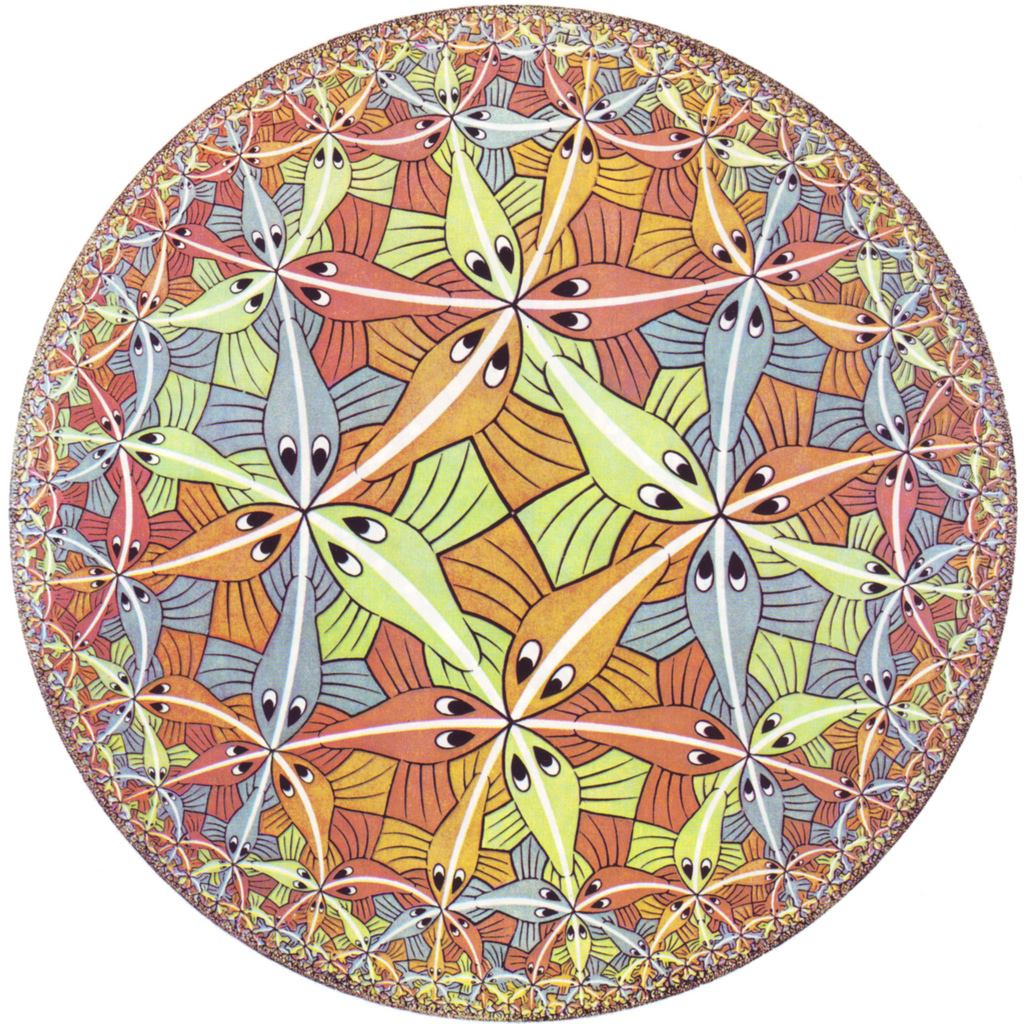
Limite del cerchio III, 1958, xilografia
Escher diceva che “i matematici non sono vecchi signori noiosi, ma allegri come ragazzi e molto giocosi”; se aveva un cruccio artistico, quindi, non esitava a parlarne con loro. Quando conobbe il matematico Harold Coxeter, per esempio, gli confidò la sua ossessione per l'infinito: come fare a rappresentarlo nello spazio limitato di un foglio? Coxeter gli suggerì di cambiare prospettiva, e di immaginare uno spazio non piano, ma curvo. In uno spazio curvo le linee hanno la forma di iperboli e tendono all'infinito verso un limite che si può rappresentare. Immaginate di vedere dall'alto una cupola senza fine: i limiti a cui le iperboli tendono prendono, tutti assieme, la forma di un cerchio.
Ecco l'idea! Escher ci si mise al lavoro, ed è così che nacquero i suoi "Limite del cerchio".
Si tratta di xilografie complesse e difficilissime, non solo per la matematica sottesa, ma per la deformazione dei disegni secondo la curvatura e secondo la scala, oltre che per l'intaglio su legno di figure anche microscopiche; "Limite del cerchio III", quella che Escher ritenne la meglio riuscita, ci colpisce però perché è buffa e giocosa, con tutti quegli strambi animaletti, i colori squillanti, le curve morbide e armoniose.
C'era di che essere soddisfatti. Era un "gioco molto serio" perfetto: un po' come la matematica.
All M.C. Escher works © the M.C. Escher Company


